Чертеж шара и геометрия сферы формулы и рисунки

Категория: Геометрия

9 426

Чертеж шара и геометрия сферы формулы и рисунки, на которых показаны фигуры образованные путем пересечения различных плоскостей.

Всякое сечение сферы плоскостью есть круг. Большой круг имеет радиус R, который получается от сечения сферы с плоскостью, проходящей через ее центр.

Через всякие две точки сферы, не являющимися противоположными концами диаметра, всегда можно провести большой круг, и только один. Меньшая дуга этого большого круга является кратчайшим расстоянием на сфере между данными точками, соединяющая эти точки (так называемая геодезическая линия на сфере) и играет на поверхности ту же роль, что прямые на плоскости.

Геометрия сферы – это поверхность шара, которая характеризуется следующими величинами:

D – диаметр шара;
R – радиус шара;
S – площадь (поверхность) сферы;
V – объем шара

Размеры представленных величин определяются по формулам:

D = 2R

S = 4πR² = πD² ≈ 12,57R² ≈ 3,142D²

V = 4/3πR³ = πD³ /6 = 1/6√S3/π ≈ 0,5236D3 ≈ 0,09403√S³

R = ½ √S/π ≈ 0,2821√S

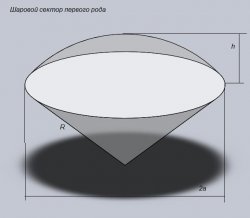
Шаровой сектор первого род – это фигура вращения сектора окружности относительно радиуса (первого рода),

S = πR(2h + a)

V = 2πR² h/3

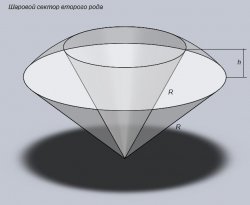
Шаровой сектор второго род – это фигура вращения вокруг диаметра, не пересекающего его дуги (второго рода)

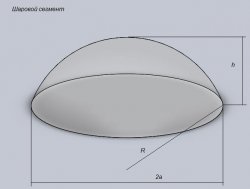
Шаровой сегмент – это часть шара, которая отсекается одной плоскостью

a² = h(2R – h)

S = π(2Rh + a²) = π(h² + 2a²)

V = 1/6 πh(3a² + h²) = 1/3 πh²(3R – h)

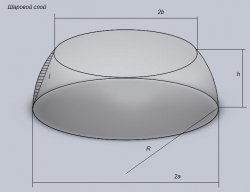
Шаровой слой – это часть шара, которая отсекается двумя параллельными плоскостями, расположенными на расстоянии h друг от друга

R² = a² + ((a² – b² – h²)/2h)²

S = π(2Rh + a² + b²)

V = 1/6 πh(3a² + 3b² + h²)

Справка:
Если V1 – объем усеченного конуса, вписанный в шаровой слой, и l – его образующая, то
V – V1 = 1/6πhl²

Заказать чертеж

Поделитесь с друзьями!